CAT 2020 Quant Questions Slot 1
Q1. How many 3-digit numbers are there, for which the product of their digits is more than 2 but less than 7?
Answer: 21
Q2. Veeru invested Rs 10000 at 5% simple annual interest, and exactly after two years, Joy invested Rs 8000 at 10% simple annual interest. How many years after Veeru’s investment, will their balances, i.e., principal plus accumulated interest, be equal?
Answer: 12
Q3. An alloy is prepared by mixing three metals A, B and C in the proportion 3: 4: 7 by volume. Weights of the same volume of the metals A, B and C are in the ratio 5: 2: 6. In 130 kg of the alloy, the weight, in kg, of the metal C is
(a) 70
(b) 96
(c) 48
(d) 84
Answer: D
Q4. On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
Answer: B
Q5. If log45=(log4y) (log6√5), then y equals
Answer: 36
Q6. Two persons are walking beside a railway track at respective speeds of 2 and 4 km per hour in the same direction. A train came from behind them and crossed them in 90 and 100 seconds, respectively. The time, in seconds, taken by the train to cross an electric post is nearest to
(a) 87
(b) 82
(c) 75
(d) 78
Answer: B
Q7. The number of real-valued solutions of the equation 2x+2-x = 2 – ( x- 2)2is
(a) infinite
(b) 1
(c) 0
(d) 2
Answer: C
Q8. If y is a negative number such that 2y2log35=5log23, then y equals.
(a) log2(1/3
(b) −log2(1/3)
(c) log2(1/5)
(d) −log2(1/5)
Answer: A
Q9. How many distinct positive integer-valued solutions exist to the equation (x2−7x+11)(x2−13x+42)=1?
(a) 6
(b) 8
(c) 2
(d) 4
Answer: A
Q10. A person spent Rs 50000 to purchase a desktop computer and a laptop computer. He sold the desktop at 20% profit and the laptop at 10% loss. If overall he made a 2% profit then the purchase price, in rupees, of the desktop is
Answer: 20000
Q11. The area of the region satisfying the inequalities |x|−y ≤ 1,y ≥ 0 and y ≤ 1 is
Answer: 3
Q12. A straight road connects points A and (B)Car 1 travels from A to B and Car 2 travels from B to A, both leaving at the same time. After meeting each other, they take 45 minutes and 20 minutes, respectively, to complete their journeys. If Car 1 travels at the speed of 60 km/hr, then the speed of Car 2, in km/hr, is
(a) 90
(b) 100
(c) 80
(d) 70
Answer: A
Q13. Among 100 students, x1 have birthdays in January, x2 have birthdays in February, and so on. If x0=max(x1,x2,…,x12), then the smallest possible value of x0x0 is
(a) 9
(b) 10
(c) 8
(d) 12
Answer: A
Q14. The mean of all 4 -digit even natural numbers of the form ‘aabb’, where a >0, is
(a) 5050
(b) 4466
(c) 5544
(d) 4864
Answer: C
Q15. Leaving home at the same time, Amal reaches office at 10: 15 am if he travels at 8 km/hr, and at 9: 40 am if he travels at 15 km/hr. Leaving home at 9: 10 am, at what speed, in km/hr, must he travel so as to reach office exactly at 10 am ?
(a) 13
(b) 14
(c) 12
(d) 11
Answer: C
Q16. A train travelled at one-thirds of its usual speed, and hence reached the destination 30 minutes after the scheduled time. On its return journey, the train initially travelled at its usual speed for 5 minutes but then stopped for 4 minutes for an emergency. The percentage by which the train must now increase its usual speed so as to reach the destination at the scheduled time, is nearest to
(a) 58
(b) 67
(c) 61
(d) 50
Answer: B
Q17. If x=(4096)7+4√3, then which of the following equals 64 ?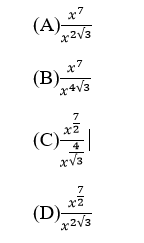
Answer: D
Q18. If f(5+x)=f(5−x) for every real x, and f(x)=0 has four distinct real roots, then the sum of these roots is
(a) 0
(b) 40
(c) 10
(d) 20
Answer: D
Q19. If a, b and c are positive integers such that ab = 432, bc = 96 and c < 9, then the smallest possible value of a + b + c is
(a) 56
(b) 59
(c) 49
(d) 46
Answer: D
Q20. In a group of people, 28% of the members are young while the rest are ol(D)If 65% of the members are literates, and 25% of the literates are young, then the percentage of old people among the illiterates is nearest to
(a) 62
(b) 55
(c) 66
(d) 59
Answer: C
Q21. A circle is inscribed in a Rhombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
Answer: B
Q22. A gentleman decided to treat a few children in the following manner. He gives half of his total stock of toffees and one extra to the first child, and then the half of the remaining stock along with one extra to the second and continues giving away in this fashion. His total stock exhausts after he takes care of 5 children. How many toffees were there in his stock initially?
Answer: 62
Q23. Let A, B and C be three positive integers such that the sum of A and the mean of B and C is 5. In addition, the sum of B and the mean of A and C is 7. Then the sum of A and B is
(a) 6
(b) 5
(c) 7
(d) 4
Answer: A
Q24. A solution, of volume 40 litres, has dye and water in the proportion 2 : 3. Water is added to the solution to change this proportion to 2 : 5. If one-fourths of this diluted solution is taken out, how many litres of dye must be added to the remaining solution to bring the proportion back to 2 : 3?
Answer: 8
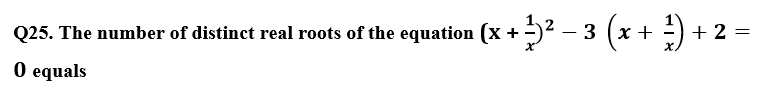
Answer: 1
Q26. A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
(a) 232
(b) 256
(c) 264
(d) 243
Answer: D
Our Address
AMS Learning Systems Private Limited
A 25/4, First Floor, Middle Circle, Connaught Place, New Delhi 110001. (Delhi Office)
Quoin Academy, 305, Rajdarshan SOC, Dada Patil Wadi, Behind ICICI ATM, Thane West. (Mumbai Office)
Contact Us
Email :info@mindworkzz.in
CALL US : Admissions –9595806833
Helpline – 9415333920/ 8376996801